200以上 正 三角形 の 公式 299769

 三角形 三角形の面積の公式をご紹介します。 公式の個数は、「底辺と高さが分かっている三角形」と「正三角形」の2個になります。三角形の公式は、小学5年生にて指導される内容となります。 出典：小学校算数科の内容の構成文部科学省 ヘロンの公式の証明と使用例 ヘロンの公式とは，三角形の3辺の長さから面積を求めるための公式です。 3辺の長さが a, b, c a, b, c a,b,c の三角形の面積 S S S は, s = a b c 2 s=\dfrac {abc} {2} s = 2a b c 難関大学で頻出テーマの正\(n\)角形ですが、意外とその対処法を知らない受験生は多いです。この記事を読んで、その対処法を完璧にしてしまいましょう！ 三角形に分割せよ 正\(n\)角形を前にしてすべきことは、ただ1つです。 Point あ 正\(n\)角形 → \(n\)個の三角形に分割 \(n\)個の三角形

正三角形の面積計算 ゆるゆるプログラミング

正 三角形 の 公式

正 三角形 の 公式-与えられた三角形の辺の長さを把握する この場合、a = 5、 b = 5、そしc = 5となります。 つまり、3辺の長さが等しいので、これは正三角形です。ただし、正三角形でもそうでなくても、この計算式は直角边 a 的长度就变成了边长的1/2，直角边 b 就是所求的三角形的高。 以边长为8的等边三角形为例，其中 c = 8 ， a = 4 。 4 将数值代入勾股定理的公式，求出b2。

正三角形面積公式 簡単公式 正三角形の面積の求め方がわかる3ステッ Rlnew

正三角形 ホーム / 数学公式集 / 三角形三角関数の三角形への応用 ここからは、三角関数を利用した三角形の公式をまとめています。 正弦定理 三角形の3つの頂点を通る円はただ1つに決まり、これを外接円といいます。この外接円の半径を r として、次の正弦定理が成り立ちます。正三角形の辺を入力 辺 a = 1 面積 S = 0433 正三角形の辺を入力 辺 a = 23 面積 S = 2291 このように正三角形の面積を計算してみました。 その他のサンプルプログラムも合わせてご覧ください。 C言語のサンプルプログラム集

 直角二等辺三角形だけど、さっきの計算問題と同じだ。 三平方の定理の公式を使ってやると、 x² = 1² 1² x = √2 になるぞ。 この直角二等辺三角形からピタゴラスは「無理数」を発見したと言われているんだ。正三角形の面積 1辺の長さから正三角形の面積，以下のように三角形の3辺の長さを代入することで面積を計算する公式です。 5/6/19 正三角形の高さと面積を求める公式について説明します。 作者 數學部屋 ・正三角形の面積計算 1辺の長さaの正三角形の 今回のテーマは正三角形の2大公式です。 これらの公式をおぼえれば、正三角形の高さと面積を瞬間的に出すことができます。 まずはこちらの例題を、一般的なやり方で解いてみましょう。 正三角形の高さにあたる線を引き、底辺との交点をOとします。 二等辺三角形の性質により、高さにあたる垂線は底辺を二等分するので、直角三角形ABOの底辺は3cmです。 ∠ABO

语音编辑锁定讨论上传视频 本词条由"科普中国"科学百科词条编写与应用工作项目审核。 经过三角形各顶点的圆叫做三角形的外接圆，表示三角形外接圆半径的方法有：1用三角形的边和角来表示它的外接圆的半径；2．用三角形的三边来表示它的外接圆的半径；3 用三角形的三边和面积表示外接圆半径的公式等。 中文名 外接圆半径公式 所属学科 数学 相关概念三角形の面積を求めるためには 一旦、平行四辺形の面積を求め それを半分にしている。 だから、2で割る必要があるんですね！ 忘れないように覚えておきましょう(^^) 三角形の面積を求める問題 それでは、三角形の面積公式を使って問題を解いていきましょう。外接圓和內切圓半徑 設外接圓半徑為 R {\displaystyle R} ， 內切圓半徑為 r {\displaystyle r} ，則： R = a b c ( a b c ) ( b c − a ) ( a c − b ) ( a b − c ) = a b c 4 {\displaystyle R= {\frac {abc} {\sqrt {\left (abc\right)\left (bca\right)\left (acb\right)\left (abc\right)}}}= {\frac {abc} {4\triangle }}}

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

三角形の公式 Wakatta

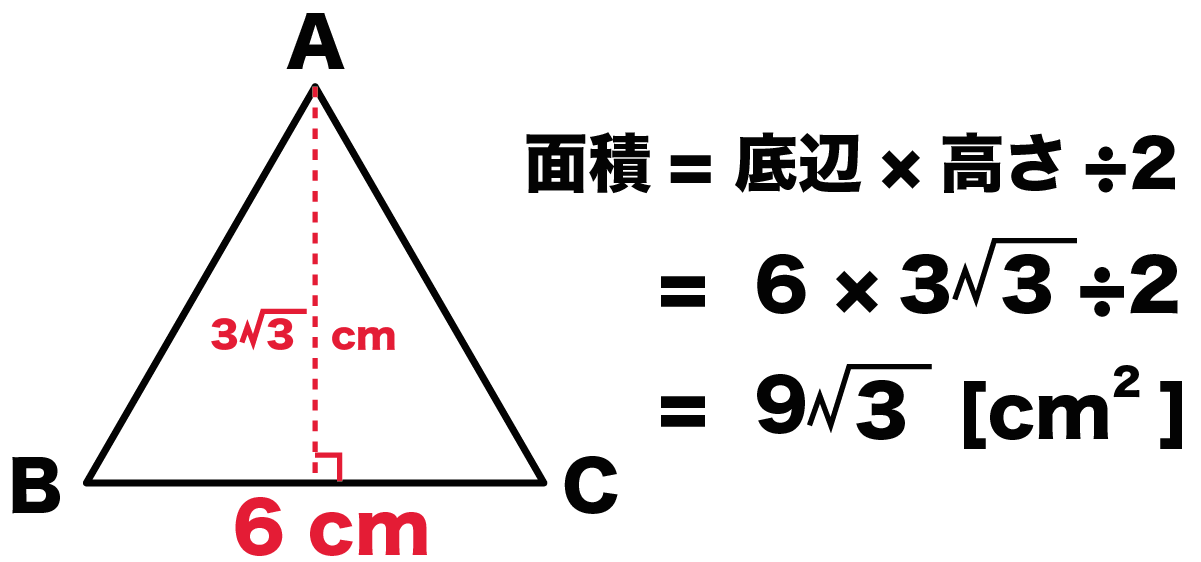
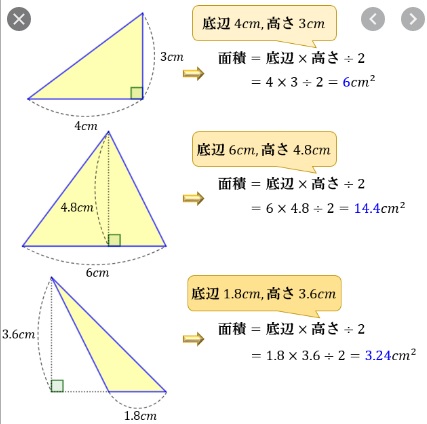
 ここでは、代表的な三角形の面積の公式 つを紹介します。 公式①底辺 × 高さ ÷ 2 まず つ目は、 底辺 と 高さ を使った最もオーソドックスな公式です。正三角形の面積を求める公式 公式は = で、 は正三角形の1辺の長さです。正三角形の高さと面積の求め方 手順① 正三角形を半分にする 手順② 直角三角形の比を使って高さを求める 手順③ 高さを利用して面積を求める 演習問題で理解を深める！ 正三角形の高さ、面積の求め方 まとめ 数学の成績が落ちてきたと焦ってい

簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

アスクル アムス 三角のファブリックパネル 正三角形30cm 1セット 10枚 直送品 通販 Askul 公式

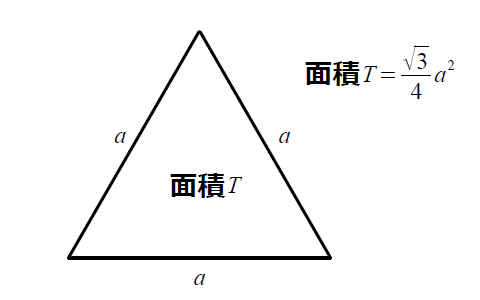
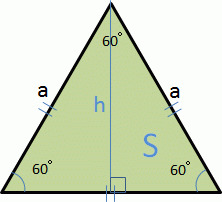
正三角形 提出时间 约17世纪 应用学科 数学，几何 边长公式 C=3a 面积公式 S=(√3)/4*a^2 第一：直角三角形边长公式：c²=a²b² ：已知三角形两条直角边的长度 ，可按公式c²=a²b²计算斜边。 2/4 第二：直角三角形边长关系： 1、两边之和大于第三边；2、直角三角形中两直角边的平方和等于斜边的平方 (c²=a²b²）。 3/4 正三角形面积公式为： S= (√3)a²/4，（S是三角形的面积，a是三角形的边长） 1、三角形面积公式为：S= (1/2)ah （S是三角形的面积，a是三角形的一条边，h是这条边上的高）

三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典

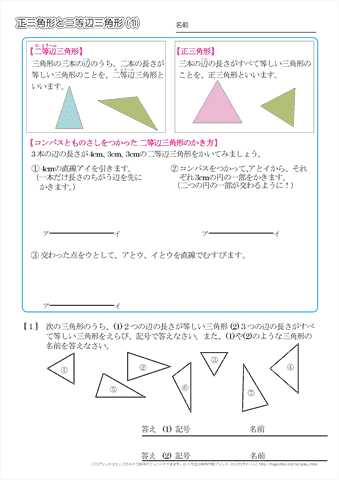
小学３年生の算数 三角形 正三角形や二等辺三角形 練習問題プリント ちびむすドリル 小学生

 1、三角形面积公式为：S= (1/2)ah （S是三角形的面积，a是三角形的一条边，h是这条边上的高） 2、正三角形，三条边相等，三条边上的高也对应相等，边长为a，高为h，则h= (√3)a/2 所以可推导出正三角形的面积S= (1/2)ah= (√3)a²/4 等边三角形（又称正三边形三角形の面積（3辺からヘロンの公式） 三角形の面積（1辺と2角から） 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積（4辺の長さから） 台形の1辺・面積（3辺の長さと高さから） ひし形の面積 平行四辺形の面積（底辺と高さから）正多角形の面積導出には、sinで表す三角形の面積公式 1 2 sin θ a b を使用します

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun

 The sum of all the angles of a triangle is 180 degrees 三角形の角度の合計は180度です The angles of an equilateral triangle are all 60 degrees 正三角形の角度は、すべて60度です #正/倒等腰三角形的输出# 要输出的三角形形状为下图 一 正三角形的输出 代码 分析 1因为图中需要打出空格数,所以要找空格数之间的关系 2找出行数,列数,空格数之间的关系(空格数一般都和行数有关系) 3注意for循环嵌套中的花括号的位置 例90秒ワンポイント授業シリーズ番外編High Speed Mathematics Ⅳ 「正三角形の2大公式」三平方の定理を学ぶと、いろいろな図形の便利な公式が

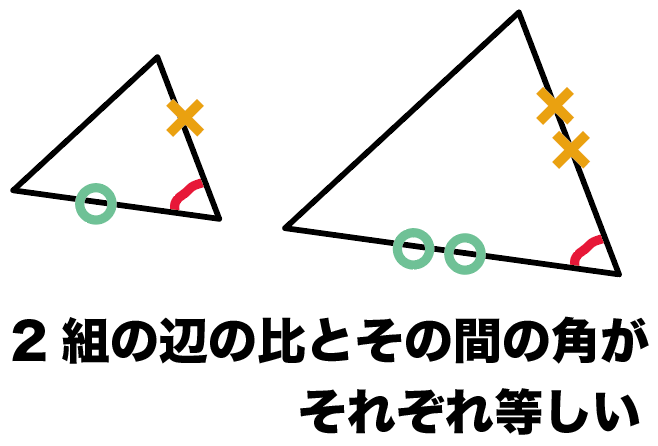
簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

正三角形面積公式 簡単公式 正三角形の面積の求め方がわかる3ステッ Rlnew

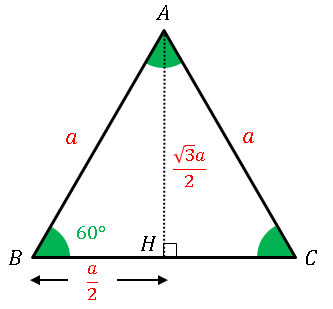
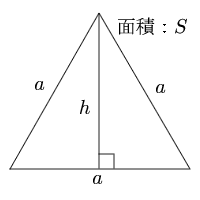
 正三角形と二等辺三角形の定義をみてみると、 2つの辺が等しい⇒二等辺三角形 3つの辺が等しい⇒正三角形 となりますが、3つの辺が等しいという事は2つの辺が等しいともいえますね。 そのため、正三角形というのは二等辺三角形の一種なのです。 2つの辺が等しい二等辺三角形の中の、さらにもう1辺も等しいレア三角形。 それが正三角形です。 二等辺三角形正三角形の面積，正四面体の体積を求める公式 (i)1辺の長さが a a a の正三角形の面積 S S S は， S = 3 4 a 2 S=\dfrac{\sqrt{3}}{4}a^2 S = 4 3 a 2指定された正三角形の高さから公式で1辺の長さ，面積を計算し表示します。 1辺の長さaが1の正三角形 高さ h： 面積 S：

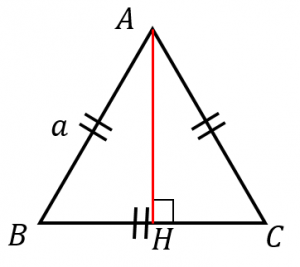
正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学

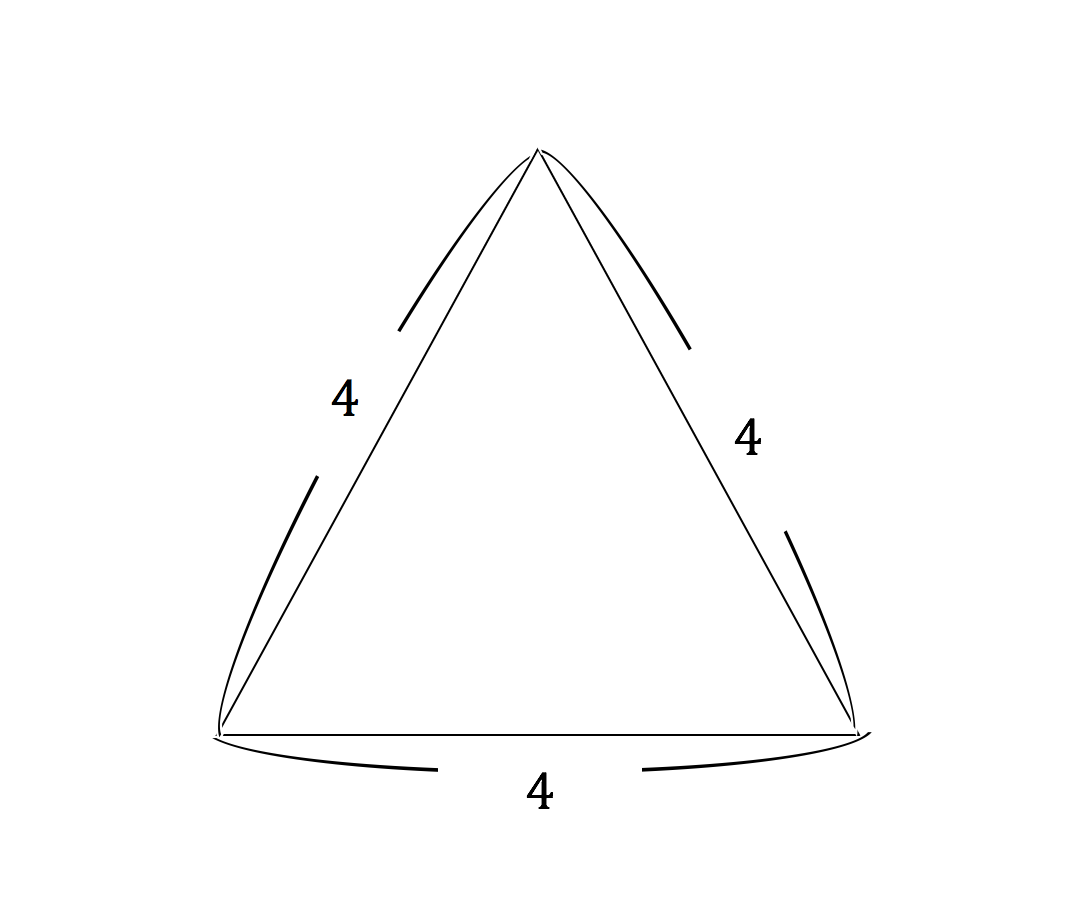
3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ

正三角形の面積 三角形の面積（底辺と高さから） 三角形の面積（2辺と夾角から） 三角形の面積（3辺からヘロンの公式） 三角形の面積（1辺と2角から） 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積（4辺の長さから）正三角形の特徴、特性、公式および面積 A 正三角形 それは3辺を持つ多角形です。 つまり、それらは同じ基準を持っています。 その特性のためにそれは正三角形の（等辺）の名前を与えられました 三角形は、3つの側面、3つの角度、3つの頂点で形成され球面三角法の基本公式 abc を球面三角形とし辺 bc, ca, ab の長さをそれぞれ a, b, c とする。弧 ab を含む大円が乗る平面と弧 ac を含む大円が乗る平面のなす角を a とする。これは、点 a における2つの大円の接ベクトルのなす角ともいえる。

直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学

正三角形を2等分する最短の境界線を求めよ 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog

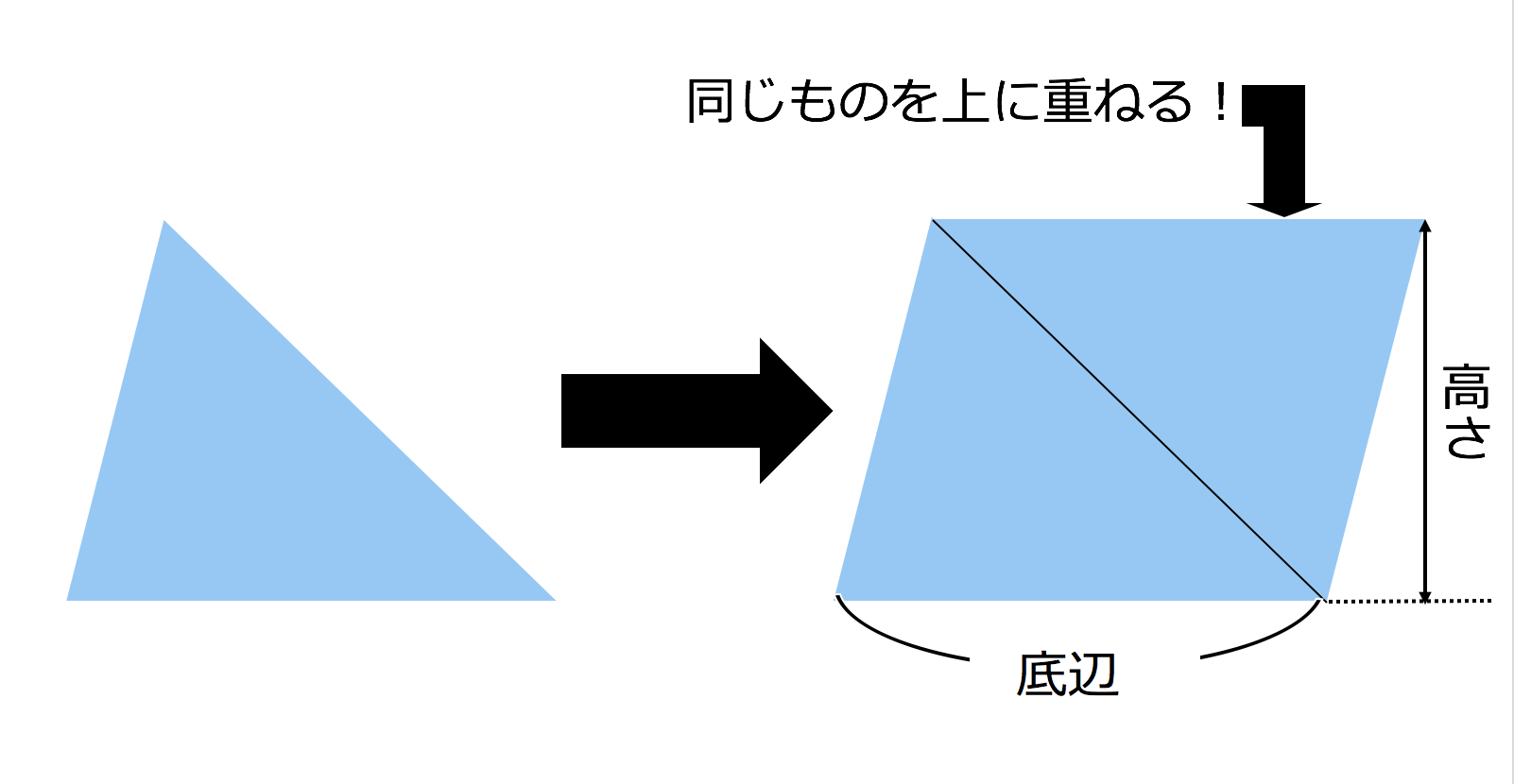
三角形の面積の公式 三角形の一辺の長さを『底辺』とし、頂点から底辺に向かって垂直に下ろした線の長さを『高さ』と言います。 このとき三角形の面積は『底辺×高さ ÷2 ÷ 2 』で求めることができます。 例題を見てみましょう。 例題 底辺 6cm 6 c mA = 3 4 a 2 {\displaystyle A= {\frac {\sqrt {3}} {4}}a^ {2}} 外接圓 的半徑 R = 3 3 a {\displaystyle R= {\frac {\sqrt {3}} {3}}a} 內切圓 的半徑 r = 3 6 a {\displaystyle r= {\frac {\sqrt {3}} {6}}a} 以上公式可由 勾股弦定理 推導而得。 正三角形的垂足和其底邊的中點共點，因此正三角形的高也是其底邊的 中垂線 及 中線 ，高也會將頂點所的在的角平分。

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ

三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

正三角形の性質 角度 面積 周の長さ 対称性

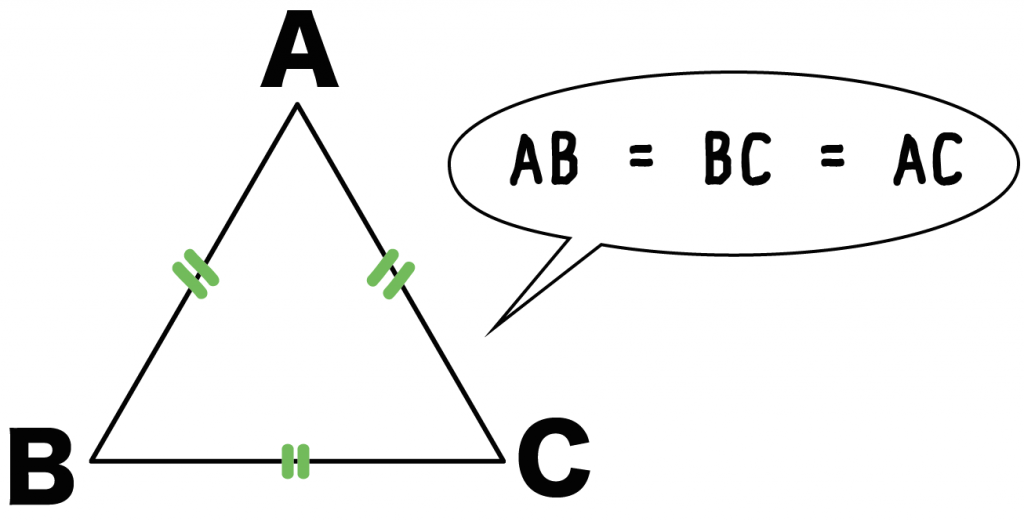
中2数学 3分でわかる 正三角形の定義とは Qikeru 学びを楽しくわかりやすく

三角形の面積と公式 面積計算機

正三角形の面積 雑学のソムリエ

直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう

正三角形 直角三角形 の韓国語は 三角形の種類や特徴を表現してみよう 気になるkorean

直角三角形 Wikipedia

一辺が9センチの正三角形の高さをもとめてください式もおねがいします 三平 Yahoo 知恵袋

直角三角形とは 定義や定理 辺の長さの比 合同条件 受験辞典

正三角形 Wikipedia

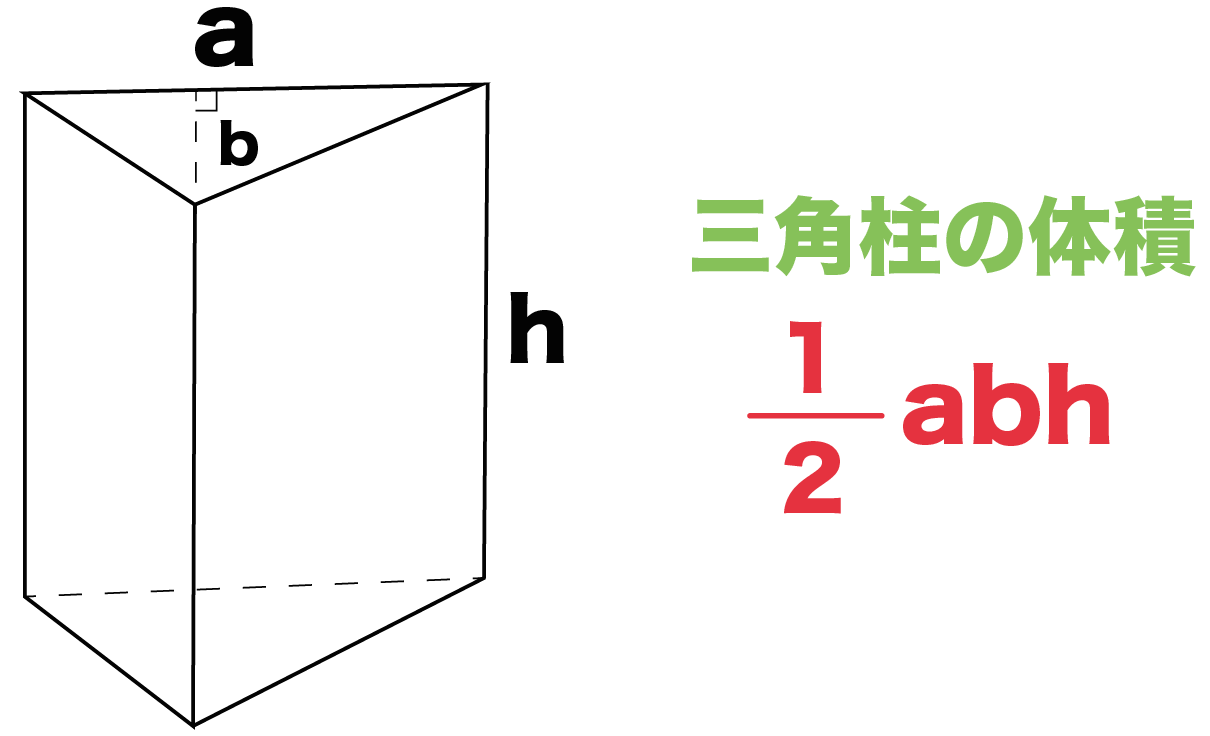
簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

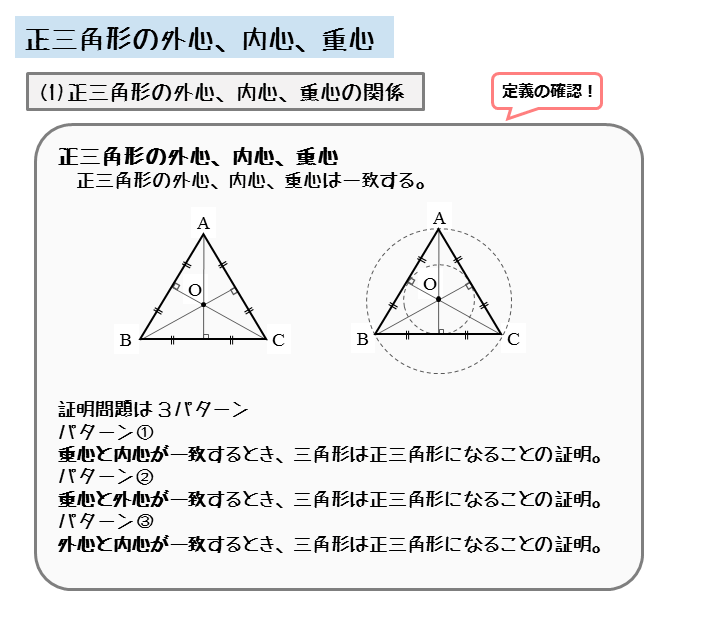
図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん

面積の求め方 計算公式一覧

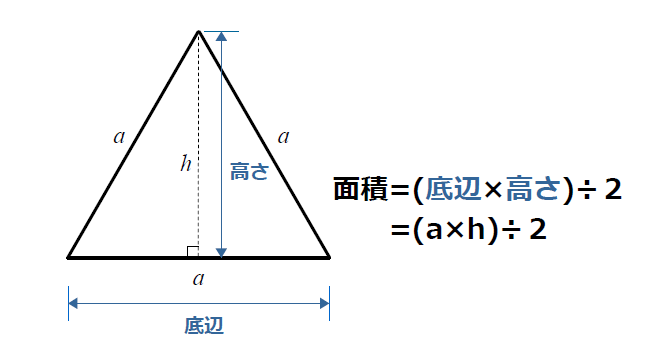
正三角形の面積計算 ゆるゆるプログラミング

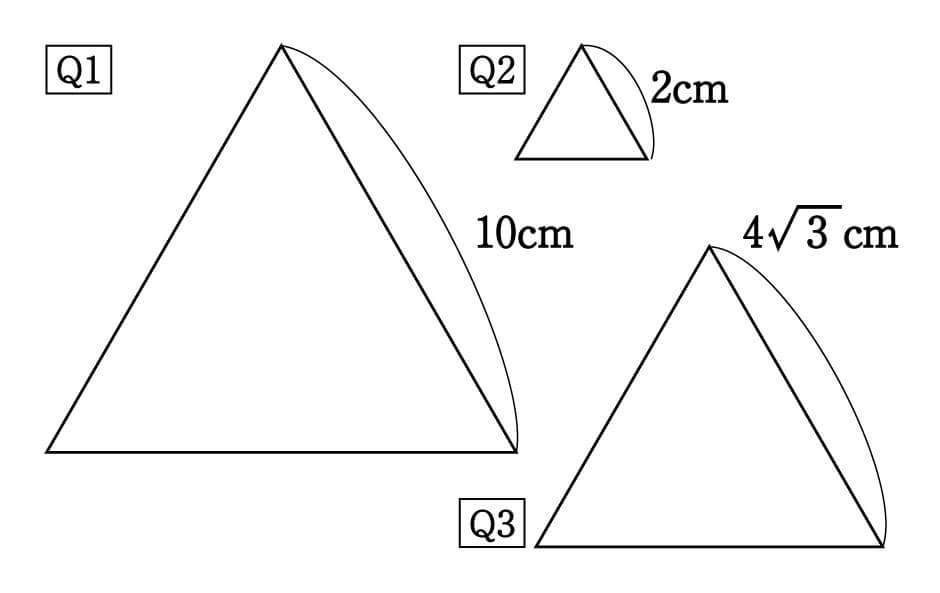
数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

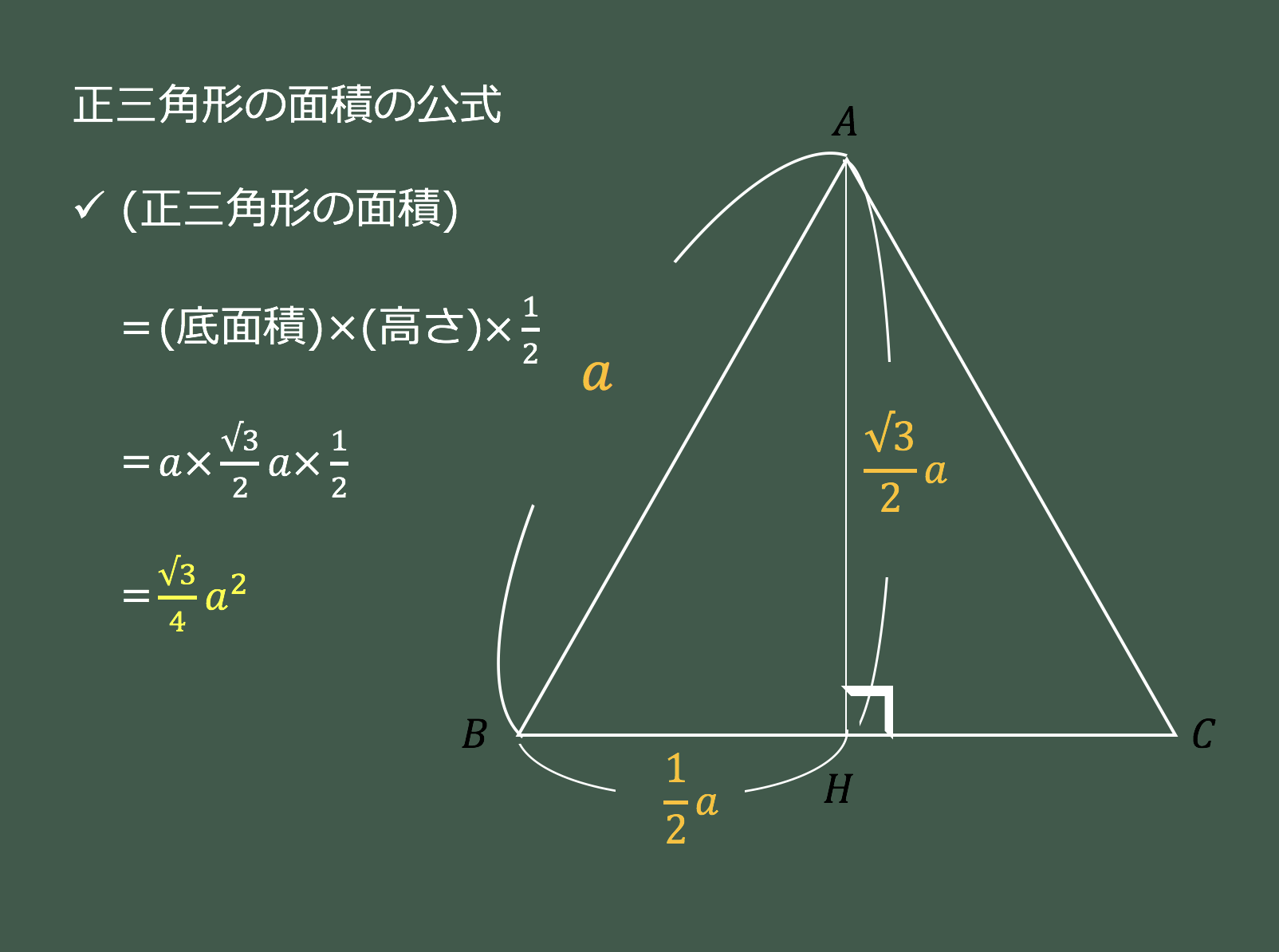
3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ

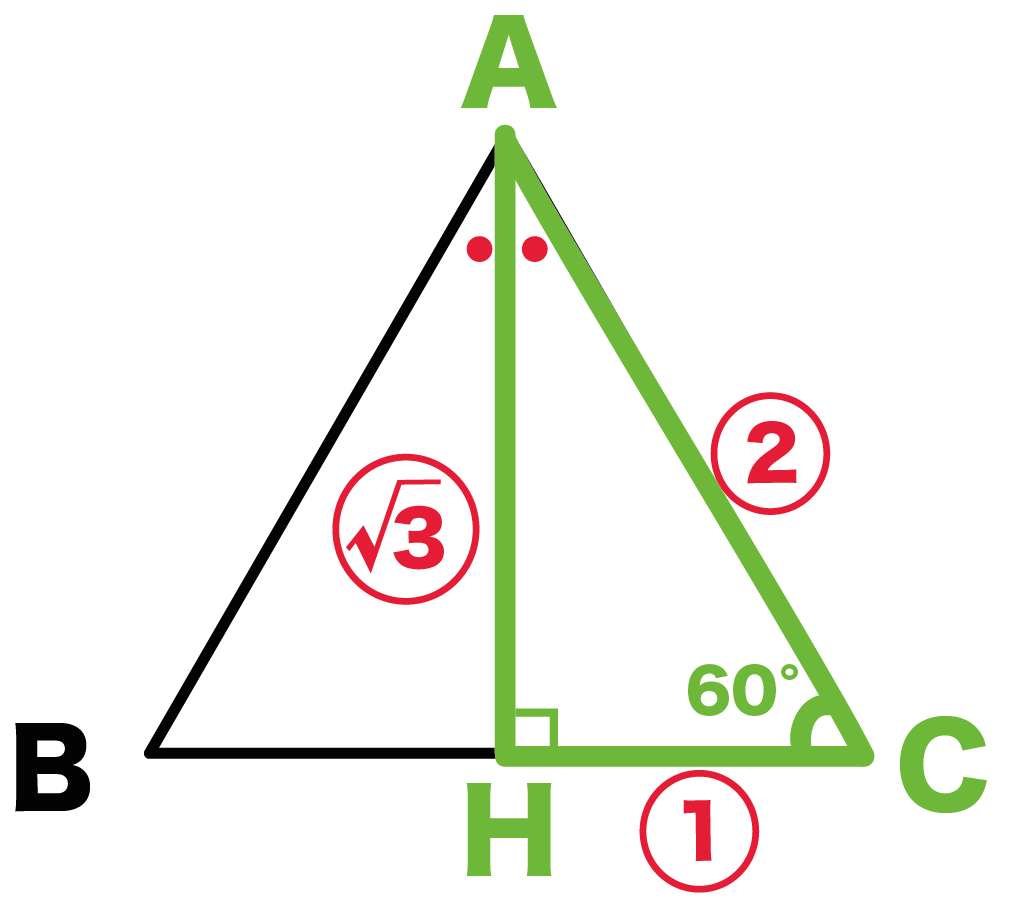
簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

三角形 を英語で説明しよう 正三角形は 二等辺三角形は 話す英語 暮らす英語

作図 円に内接する正三角形の作図方法とは 数スタ

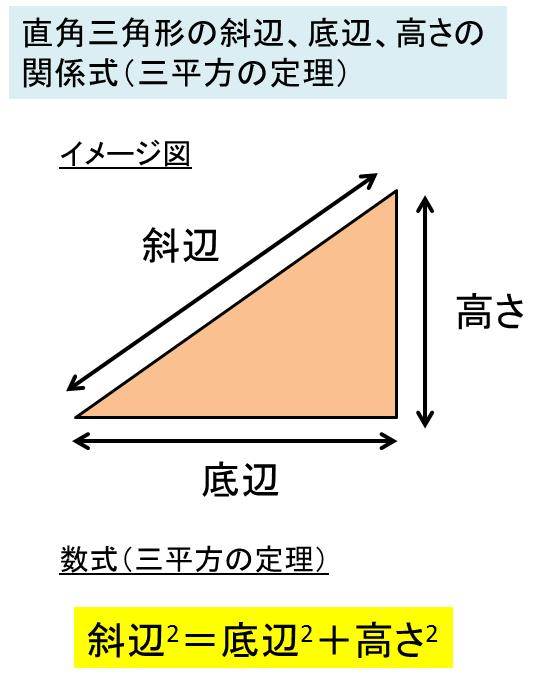
Excel 三角形の斜辺の長さ 高さ 底辺の長さを残りの2辺からする方法 直角三角形の辺の求め方

二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比

正多面体の種類と性質 面 辺 頂点の数の公式 数学fun

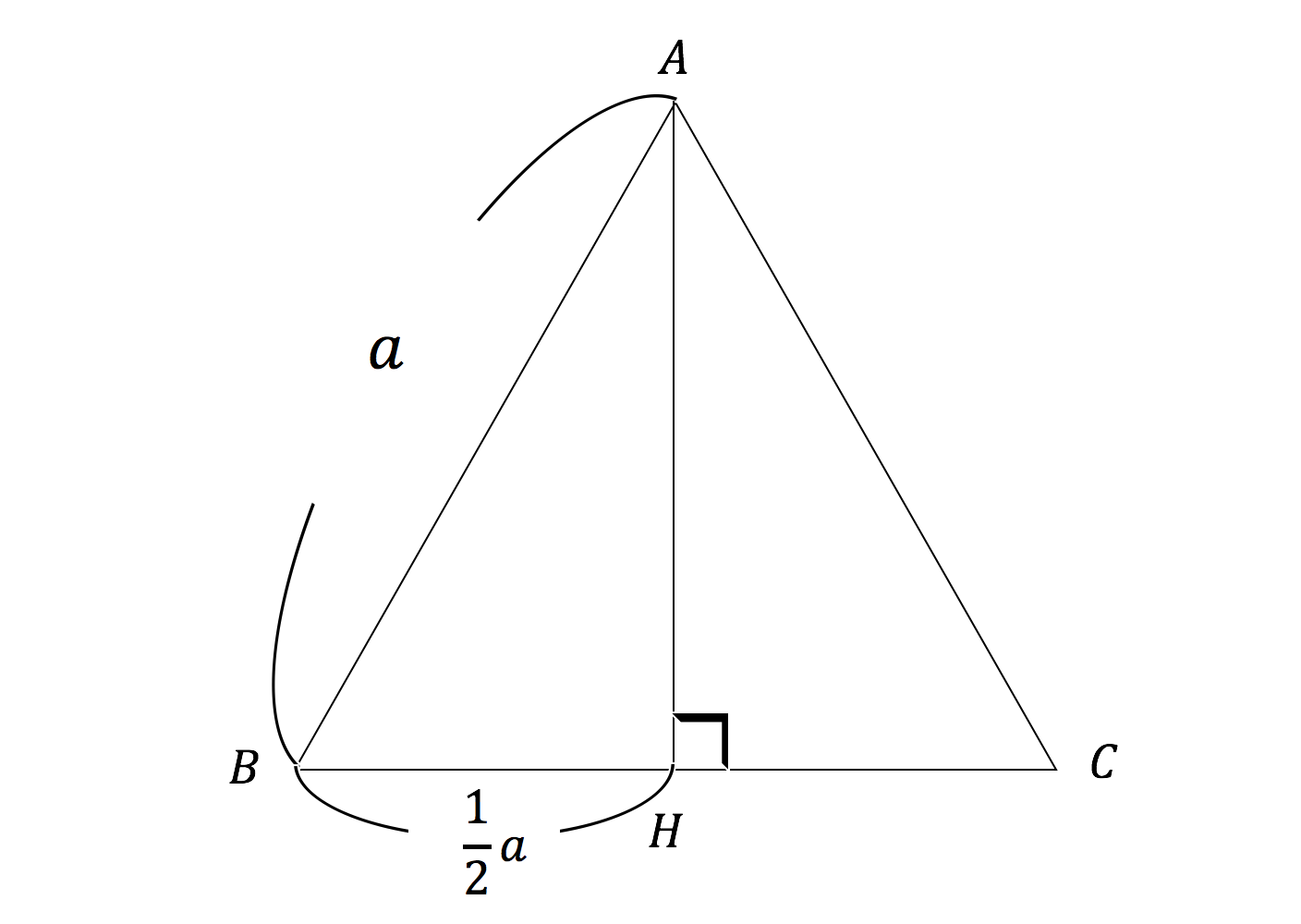
3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ

面積が 3の正三角形の一辺の長さは について 教えてください Clear

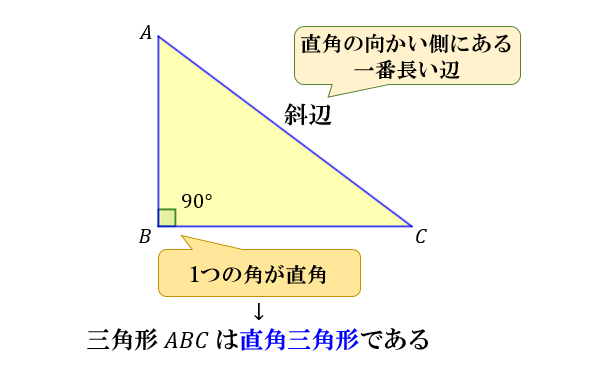
直角三角形の辺の長さ 合同条件 面積について アタリマエ

正三角形の面積計算 ゆるゆるプログラミング

1

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

正三角形の高さを求める3つの方法と求め方がわかる3ステップ 言葉 雑学 歴史を知るならmayonez

直角三角形の合同条件とその証明 数学fun

3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ

三平方06 正三角形の面積 Youtube

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

正三角形的高與面積計算 Math Height And Area Of An Equilateral Triangle Youtube

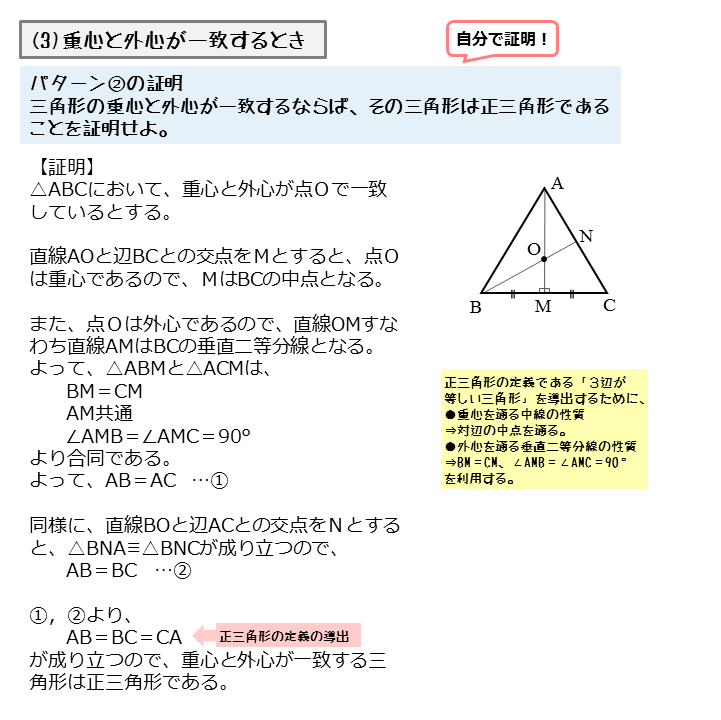
図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん

高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月

小5 面積 三角形の面積の求め方 日本語版 Youtube

正三角形の面積 高さ 辺の長さの計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ

1

三角形の面積 中学受験 塾なし の勉強法

100以上 正 三角形 の 公式 ニスヌーピー 壁紙

正三角形の面積の求め方 小学生用 高校生用 具体例で学ぶ数学

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

正三角形の面積 正四面体の体積を求める公式 高校数学の美しい物語

三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ

正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座

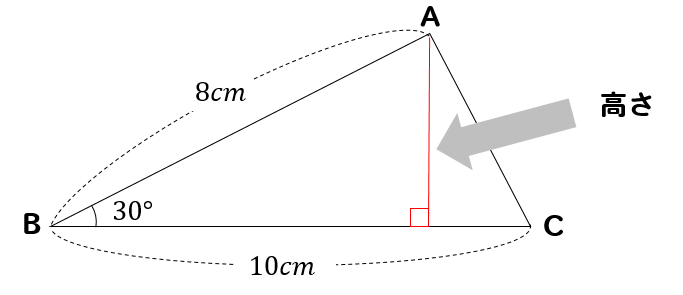
高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ

正三角形 面積の計算 計算サイト

正三角形 翰林雲端學院

二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ

正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典

3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ

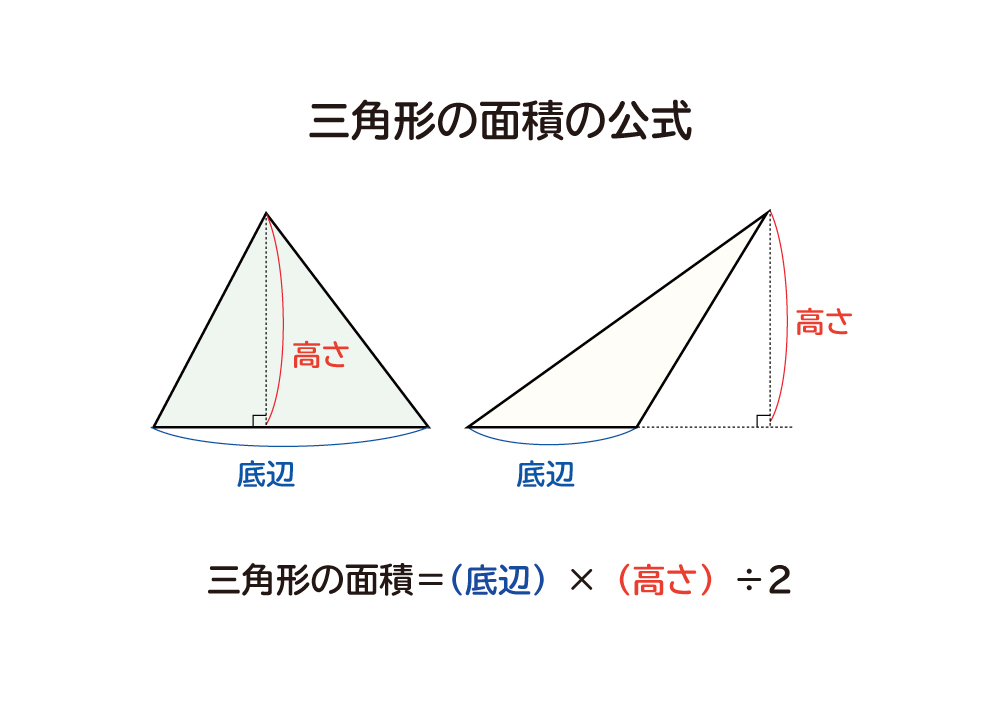
なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル

最高 50 正三角形 面積 求め方

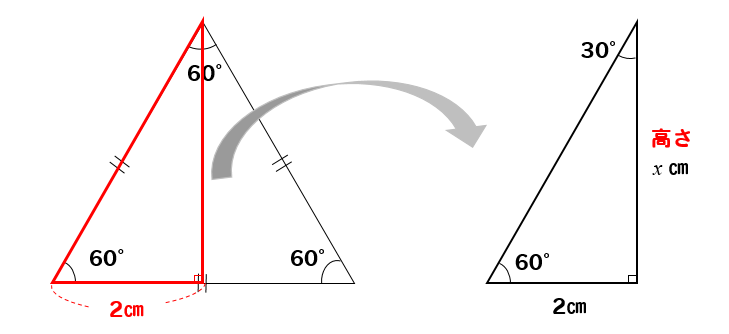
三平方の定理 正三角形の高さ 面積を求める方法を解説 数スタ

マッチ棒クイズ 図形問題3

正三角形 维基百科 自由的百科全书

正三角形周長公式 正三角形 辺から高さと面積 三角形の計算 計算サイト翻譯此網頁 Aozqkc

中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット

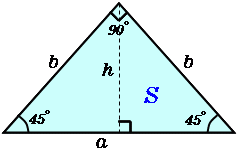
直角二等辺三角形 高精度計算サイト

直感的に求めよう 直角三角形の面積の求め方 パパが教える算数教室

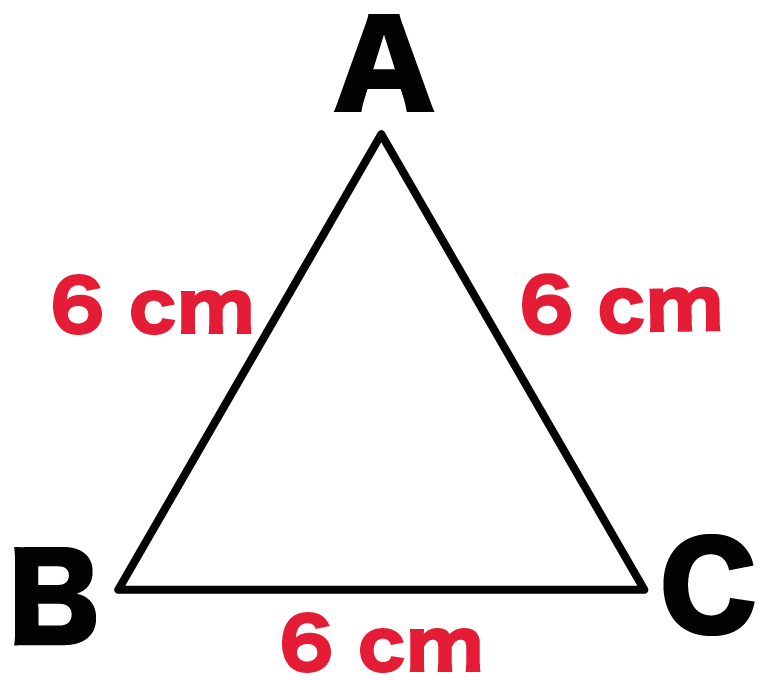
簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su

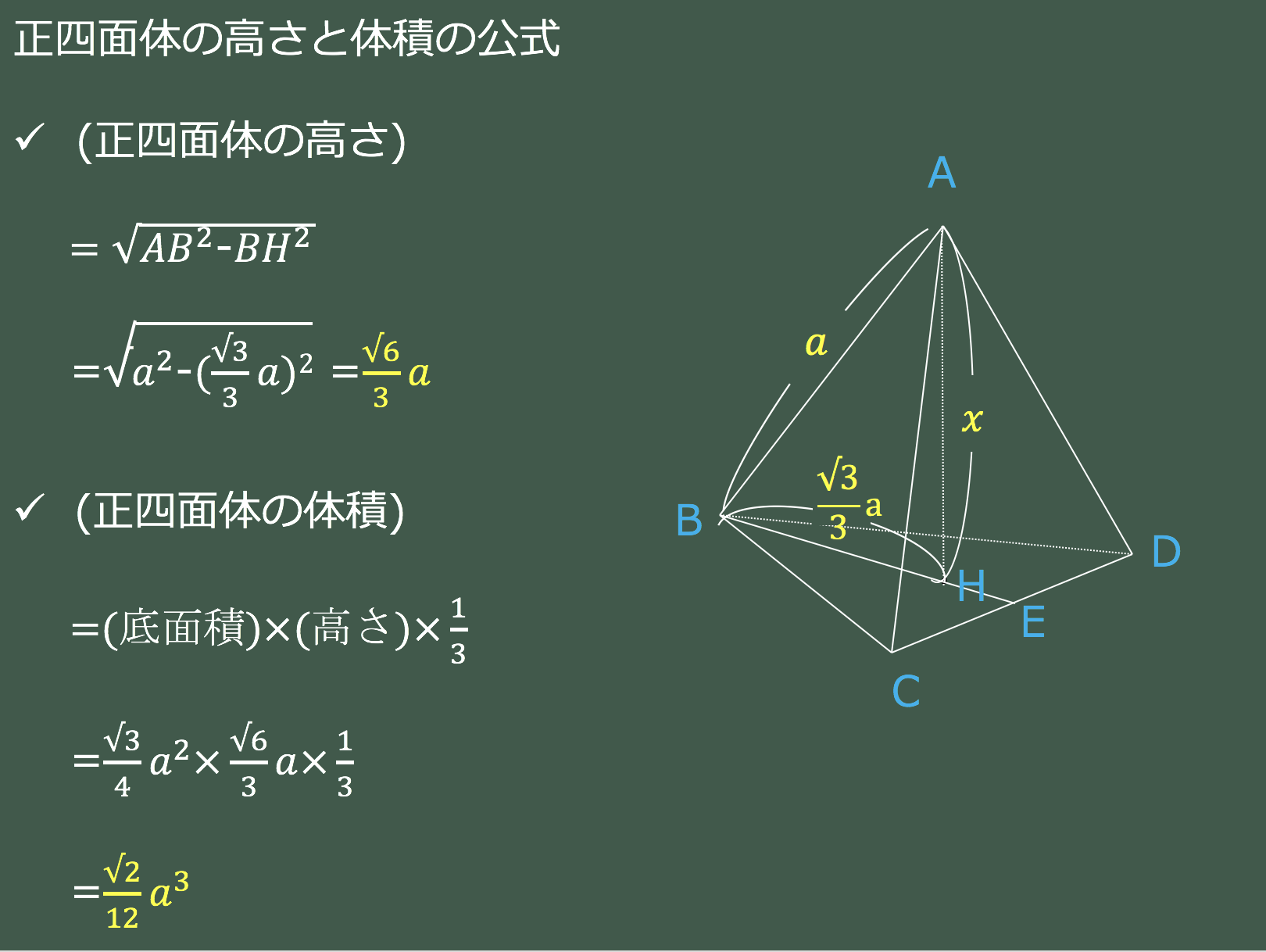
3分で分かる 正四面体の高さ 体積の求め方をわかりやすく 合格サプリ

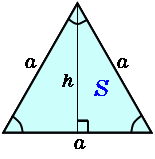
正三角形 高精度計算サイト

三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube

簡単 正三角形の面積公式が一瞬で分かる 見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

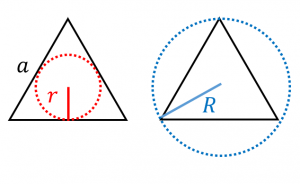
正三角形の内接円の半径と外接円の半径 具体例で学ぶ数学

高校数学a 正多角形内の三角形の個数 二等辺三角形 正三角形 直角三角形 鈍角三角形 鋭角三角形他 受験の月

3

数学の基礎 知ってる人は5秒で解ける正三角形の面積 Youtube

数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

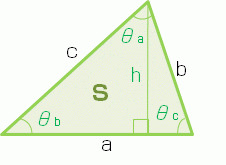
三角形の公式 Wakatta

必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ

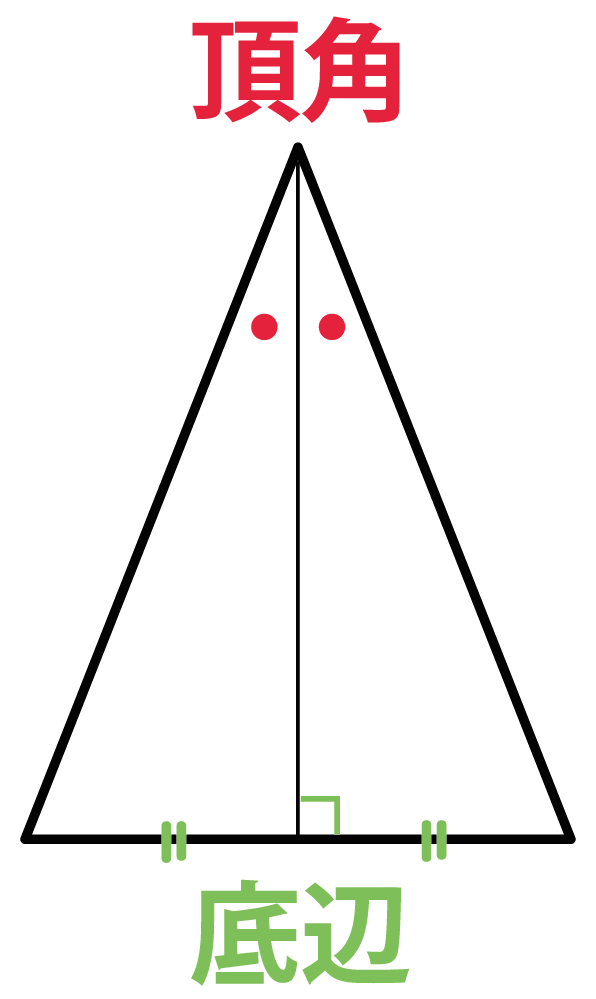
簡単公式 正三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

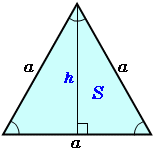
正三角形の面積 高精度計算サイト

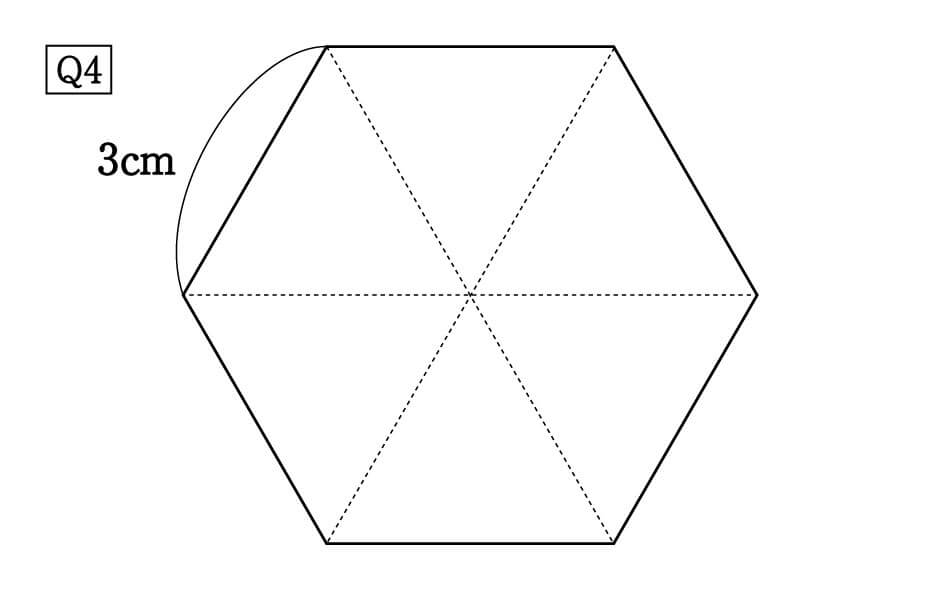
数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学

翻轉學習影片 國中 數學 三角形基本性質 正三角形

簡単公式 正三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

1

正三角形高面積 正三角形の公式 高さ 面積 Elleve